澎湃新闻记者 舒怡尔 王亚赛

　　学数学的过程，就像是不断往塔尖攀爬的过程。一路上不断有人停下，无论你是停在鸡兔同笼、立体几何、概率还是微积分，亦或是更高处，普通人总有一天会停下。

　　“挂谷猜想”是那个塔尖上的问题。

　　6 月 17 日至 19 日，数学家王虹在北京大学举行了三天讲座，讲述她是如何解开百年难题“挂谷猜想”的。“北大韦神”韦东奕在前排听了三天，出圈的是王虹和韦神探讨证明中的一个细节的视频，如同一段“加密通话”，说的虽是中文，却让人啥也听不懂。

　　王虹在北大授课

　　那么，挂谷猜想究竟是什么？

　　挂谷猜想的原型是一个很有趣的场景：一个武士在上厕所时遭到敌人袭击，矢石如雨，而他只有一根短棒，为了挡住射击，需要将短棒旋转一周 360°（支点可以变化）。但厕所很小，应当使短棒扫过的面积尽可能小。面积可以小到多少？

　　数学家将这个场景转换为：有一根长度为 1 的针，将它在平面上旋转一周（支点可以变化），它扫过的最小面积是多少？答案非常反直觉，数学家证明，扫过的面积可以无限趋近于 0。

　　如果把挂谷猜想扩展至三维空间呢？

　　三维空间中的一个挂谷集合，图源：Quanta Magazine

　　在三维空间中，如图所示，针扫过的空间可以是一个球体，也可以比球体小得多（图中的红色部分），但它的体积究竟可以有多小呢？如果这根针没有宽度的话，空间的体积最小可以是 0，推衍到高维空间中也是如此。

　　挂谷集合即为 n 维空间中可以容纳指向各个方向的长度为 1 的针的集合。数学家进一步追问：挂谷集合的“维数”可以是多少？数学中常用的分形维数有豪斯多夫（Hausdorff）维数和闵可夫斯基（Minkowski）维数。王虹和合作者扎尔证明了三维空间中的挂谷集合的豪斯多夫维数和闵科夫斯基维数等于 3. 这意味着即便挂谷集合的体积可以无限小，但挂谷集合仍然“很大”，“在某种意义上填满了空间的大部分”。

　　曾获数学界的最高奖项“菲尔兹奖”的华人数学家陶哲轩评价王虹和扎尔的论证过程“像在完善一台永动机，充满了魔幻色彩”，开辟了几何测度论的新研究范式。莱斯大学数学家内茨·卡茨（Nets Katz）认为“这可是百年一遇的数学突破啊！”

　　因此，今年只有 34 岁的王虹成为2026 年“菲尔兹奖”的热门人选。如果预言成真，那么她将成为首位获奖的中国籍数学家，也是史上第三位获奖的女数学家。

　　华人数学家的 100 年

　　“菲尔兹奖”有数学界的“诺贝尔奖”之称，旨在表彰有卓越贡献且年龄不超过 40 岁的年轻数学家，每四年在国际数学联盟的国际数学家大会上颁发，获奖者自动成为大会的受邀报告人。在学术界，受邀成为国际数学家大会的报告人，是一种对数学家成就的肯定——这些报告代表国际数学界的最高水平。

　　我们不妨梳理一番 1897 年至 2022 年大会邀请的数学家名单，来一窥一百多年来华人数学家的发展。

　　第一位参加大会的中国人是周培源，是一位物理学家。1928 年，他去德国研究量子力学，离开学还有一段时间，便取道巴黎前往意大利参加大会，在会上宣读了他关于广义相对论的博士论文。1950 年，陈省身受邀去大会做 1 小时报告。此后数年，华人数学家逐渐登上国际舞台，其中有 110 名男性，13 名女性，女性仅占 11%。

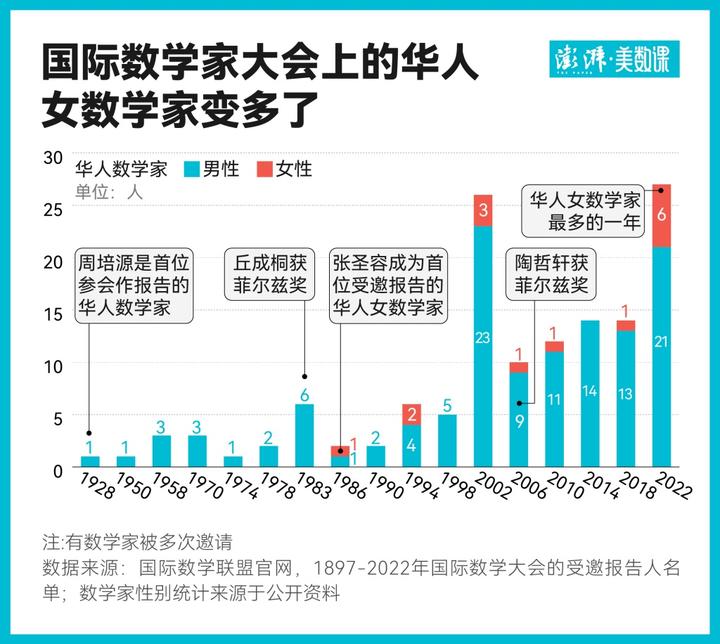
　　1986 年，张圣容受邀在大会上作 45 分钟报告，成为首位被邀请的华人女数学家，2002 年在北京举办的数学家大会上，她成为大会一小时报告人（每次只有 21 位），同年，中国科学院院士、女数学家胡和生教授第一次成为受邀报告人，那年她 74 岁。实际上，华人数学家首次参会做报告的平均年龄是 45 岁，除去 1928 年的物理学家周培源，参会的最年轻的华人数学家是 1978 年的丘成桐，才 29 岁，隔了一届他便拿了菲尔兹奖。若王虹明年夺得菲尔兹奖，她的首次参会报告年龄是 35 岁，也是非常年轻。

　　如果我们细看近几届参会的华人数学家，会发现 1982 年前后出生的数学家尤其“多”，如恽之玮、朱歆文、张伟等，他们是“北大黄金一代”。张寿武教授在评价北大数学“黄金一代”时，曾说：“厉害就厉害在他们不是一个人，而是一批人，他们有什么东西不懂，就马上打电话给同学，同学也是另一行的高手，马上就知道是怎么回事了，他们之间不是相互竞争者，而是合作者。”

　　参会报告的华人数学家中，本科就读于北大数院的有 24 人，远超其他院校，第二、三名分别为台湾大学、清华大学和中国科技大学。

　　《Quanta Magazine》的一篇讲述挂谷猜想的科普文章写道： “调和分析中三个不朽的猜想组成的塔楼，都矗立在挂谷猜想之上。如果挂谷猜想被证伪，整座塔都会轰然倒塌。但既然王虹已经证明了这一点，数学家们或许能够沿着塔向上攀登，利用挂谷理论来逐步建立起这些更雄心勃勃的猜想的证明。”调和分析是数学中的一个分支，它被应用在诸多领域，如信号处理、量子力学和神经科学等。

　　数学的塔尖被王虹拔高了一点，这或许比菲尔兹奖更重要。丘成桐说：“我对数学的本质更感兴趣，而不是这些荣耀。我喜欢研究那些让我着迷的问题，相信这些问题对数学本身很重要。”巧的是，王虹接受采访时也提到了“问题”这两个字：“（研究方向）有兴趣就读，没兴趣也没必要读……如果一个问题很吸引我的话，那它可能也具有吸引其他人的能力。”

　　本期编辑 邹姗

作者：澎湃新闻